Sparksoft

Перестановки. Упорядоченные множества, без повторений.

Перестановкой из n элементов (или n-перестановкой) называется n-элементное упорядоченное множество, составленное из элементов n-элементного множества.

Иначе: Перестановкой из n элементов (или n-перестановкой) называется размещение из n элементов по n без повторений.

Число перестановок из n элементов без повторений обозначается P_n от французского слова perturbation.

(n факториал)

Порядок важен, без повторений.

n: [ n - число элементов множества ]

Вычислить

NB! Перестановки симметричных объектов.
n различных предметов можно расположить по кругу (n - 1)! способами, а если их можно еще и переворачивать, то

различными способами.

Перестановки. Упорядоченные множества, с повторениями.

Определение: Пусть даны n₁ элементов первого типа, n₂ — второго типа, ..., n_k - k-го типа, всего n элементов. Способы разместить их по n различным местам называются перестановками с повторениями.
Их количество обозначается P_n(n₁, n₂, ..., n_k).

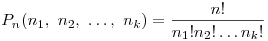Порядок важен, с повторениями.

Пример: расчет количества слов, которые можно получить, переставляя буквы в слове.

Сколько различных слов можно получить, переставляя буквы слова «комбинаторика»?
В слове «комбинаторика» 13 букв. Если бы все они были различны, то, переставляя их, можно было бы получить 13! слов, но в нашем слове буквы к, о, и, а встречаются по два раза.
Обозначим их "к1", "к2", "о1", "о2", "и1", "и2", "а1", "а2".
Ясно, что слова, отличающиеся перестановкой букв "к1" и "к2" - одинаковые, так что 13! Слов разбиваются на пары одинаковых. Следовательно, если мы не различаем "к1" и "к2", то число всех слов будет равно 13!/2!.
Но эта совокупность также разбивается на пары одинаковых с точки зрения буквы "о" слов и т.д.

Слово:

Вычислить

Размещения без повторений

Определение: Подсчитаем количество способов расположить n различных элементов по k различным позициям (k < n). Такие расположения называются размещениями, а их количество, от французского слова arrangement обозначается

Число размещений n различных элементов по k различным позициям есть

Порядок важен, без повторений.

n: [ n - число элементов множества ] k: [ k различных позиций ]

Вычислить

Размещения с повторениями

Определение: Пусть даны n различных видов предметов, которые можно разместить по k различным местам, причем выбирать предметы можно с повторениями (т.е. можно выбрать несколько предметов одного вида). Такие выборки называются размещениями с повторениями.

Количество размещениями с повторениями вычисляется по формуле:

Порядок важен, c повторениями.

Пример: расчет количества возможных паролей.

Сколько различных паролей можно соcтавить из букв (a, b, c) длиной в 5 символов?
Очевидно, что для первой позиции 3 варианта, для второй 3 варианта, ..., для пятой позиции 3 варианта, следовательно Ответ: 3*3*3*3*3=3⁵

n: [ n - число элементов множества ] k: [ k различных мест ]

Вычислить

Сочетания без повторений

Определение: Сочетаниями из n различных элементов по k элементов называются комбинации, которые составлены из данных n элементов по k элементов и отличаются хотя бы одним элементом (иначе говоря, k-элементные подмножества данного множества из n элементов).

Как видим, в сочетаниях в отличие от размещений не учитывается порядок элементов. Число всех сочетаний из n элементов по k элементов в каждом обозначается